Contribuciones islámicas
Las contribuciones islámicas a las matemáticas comenzaron alrededor del año 825, cuando el matemático de Bagdad Muḥammad ibn Mūsā al-Khwārizmī escribió su famoso tratado al-Kitāb al-mukhtaṣar fī ḥisāb al-jabr wa'l-muqābala (traducido al latín en el siglo XII como Algebra et Almucabal, del cual se deriva el término moderno álgebra). A fines del siglo IX, un importante corpus matemático griego, que incluía obras de Euclides, Arquímedes (c. 285-212 / 211 a. C.), Apolonio de Perga (c. 262–190 a. C.), Ptolomeo (fl. Ad 127–145) y Diophantus, habían sido traducidos al árabe. Del mismo modo, las antiguas matemáticas babilónicas e indias, así como las contribuciones más recientes de los sabios judíos, estaban disponibles para los eruditos islámicos. Este trasfondo único permitió la creación de un nuevo tipo de matemática que fue mucho más que una mera fusión de estas tradiciones anteriores. Un estudio sistemático de métodos para resolver ecuaciones cuadráticas constituyó una preocupación central de los matemáticos islámicos. Una contribución no menos central se relacionó con la recepción y transmisión islámica de ideas relacionadas con el sistema de numeración indio, al que agregaron fracciones decimales (fracciones como 0.125 o1 / 8).
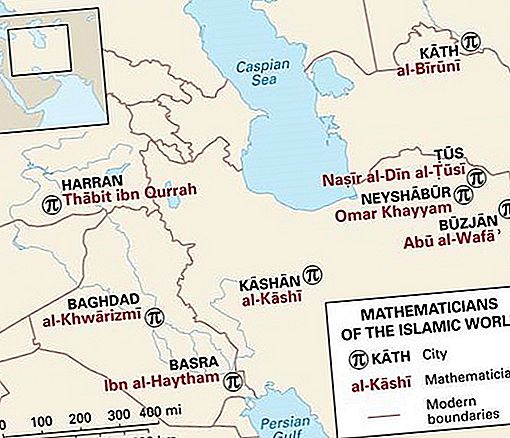
El trabajo algebraico de Al-Khwārizmī encarnaba gran parte de lo que era central para las contribuciones islámicas. Declaró que su libro tenía la intención de ser de valor "práctico", pero esta definición apenas se aplica a su contenido. En la primera parte de su libro, al-Khwārizmī presentó los procedimientos para resolver seis tipos de ecuaciones: cuadrados, raíces iguales, cuadrados, números iguales, raíces, números iguales, cuadrados y raíces, números iguales, cuadrados y números, raíces iguales, y raíces y números iguales. cuadrícula. En la notación moderna, estas ecuaciones se expresarían ax 2 = bx, ax 2 = c, bx = c, ax 2 + bx = c, ax 2 + c = bx y bx + c = ax 2, respectivamente. Solo los números positivos se consideraron coeficientes legítimos o soluciones a las ecuaciones. Además, ni la representación simbólica ni la manipulación de símbolos abstractos aparecieron en estos problemas, incluso las cantidades se escribieron en palabras en lugar de en símbolos. De hecho, todos los procedimientos fueron descritos verbalmente. Esto está bien ilustrado por el siguiente problema típico (reconocible como el método moderno de completar el cuadrado):
¿Cuál debe ser el cuadrado que, cuando se incrementa en 10 de sus propias raíces, asciende a 39? La solución es esta: reduce a la mitad el número de raíces, que en el presente caso produce 5. Esto se multiplica por sí mismo; el producto es 25. Agregue esto a 39; la suma es 64. Ahora toma la raíz de esto, que es 8, y resta de ella la mitad del número de raíces, que es 5; el resto es 3. Esta es la raíz del cuadrado que buscabas.
En la segunda parte de su libro, al-Khwārizmī utilizó proposiciones tomadas del Libro II de los Elementos de Euclides para proporcionar justificaciones geométricas para sus procedimientos. Como se señaló anteriormente, en su contexto original se trataba de proposiciones puramente geométricas. Sin embargo, Al-Khwārizmī los conectó directamente por primera vez a la solución de ecuaciones cuadráticas. Su método fue un sello distintivo del enfoque islámico para resolver ecuaciones: sistematizar todos los casos y luego proporcionar una justificación geométrica, basada en fuentes griegas. Típico de este enfoque fue el matemático y poeta persa Omar Khayyam Risālah fiʾl-barāhīn ʿalā masāʾil al-jabr waʾl-muqābalah (c. 1070; "Tratado sobre la demostración de problemas de álgebra"), en el que el conocimiento griego sobre secciones cónicas (elipses, parábolas e hipérbolas) se aplicó a preguntas relacionadas con ecuaciones cúbicas.
El uso de argumentos geométricos de estilo griego en este contexto también condujo a un aflojamiento gradual de ciertas restricciones griegas tradicionales. En particular, las matemáticas islámicas permitieron, y de hecho alentaron, la combinación irrestricta de magnitudes inconmensurables e inconmensurables dentro del mismo marco, así como la manipulación simultánea de magnitudes de diferentes dimensiones como parte de la solución de un problema. Por ejemplo, el matemático egipcio Abu Kāmil (c. 850–930) trató la solución de una ecuación cuadrática como un número en lugar de como un segmento de línea o un área. Combinado con el sistema decimal, este enfoque fue fundamental en el desarrollo de una concepción más abstracta y general del número, que fue esencial para la creación eventual de una idea abstracta completa de una ecuación.