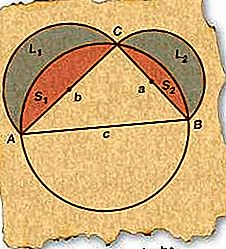
Hipócrates de Chios (fl. C. 460 a. C.) demostró que las áreas en forma de luna entre los arcos circulares, conocidos como lunes, podrían expresarse exactamente como un área rectilínea o cuadratura. En el siguiente caso simple, dos lunes desarrollados alrededor de los lados de un triángulo rectángulo tienen un área combinada igual a la del triángulo.
-
Comenzando con el ΔABC derecho, dibuje un círculo cuyo diámetro coincida con AB (lado c), la hipotenusa. Debido a que cualquier triángulo rectángulo dibujado con el diámetro de un círculo para su hipotenusa debe estar inscrito dentro del círculo, C debe estar en el círculo.
-
Dibuje semicírculos con diámetros AC (lado b) y BC (lado a) como en la figura.
-
Rotule el lunes resultante L 1 y L 2 y los segmentos resultantes S 1 y S 2, como se indica en la figura.
-
Ahora la suma del lunes (L 1 y L 2) debe ser igual a la suma de los semicírculos (L 1 + S 1 y L 2 + S 2) que los contienen menos los dos segmentos (S 1 y S 2). Por lo tanto, L 1 + L 2 = π / 2 (b / 2) 2 - S 1 + π / 2 (a / 2) 2 - S 2 (ya que el área de un círculo es π veces el cuadrado del radio).
-
La suma de los segmentos (S 1 y S 2) es igual al área del semicírculo basado en AB menos el área del triángulo. Por lo tanto, S 1 + S 2 = π / 2 (c / 2) 2 - ΔABC.
-
Sustituyendo la expresión en el paso 5 en el paso 4 y factorizando términos comunes, L 1 + L 2 = π / 8 (a 2 + b 2 - c 2) + ΔABC.
-
Como ∠ACB = 90 °, a 2 + b 2 - c 2 = 0, según el teorema de Pitágoras. Por lo tanto, L 1 + L 2 = ΔABC.
Hipócrates logró cuadrar varios tipos de lunes, algunos en arcos mayores y menores que los semicírculos, e insinuó, aunque puede no haber creído, que su método podría cuadrar un círculo entero. Al final de la era clásica, Boecio (c. Ad 470-524), cuyas traducciones latinas de fragmentos de Euclides mantendrían la luz de la geometría parpadeando durante medio milenio, mencionó que alguien había logrado la cuadratura del círculo. No se sabe si el genio desconocido usó el lunes o algún otro método, ya que por falta de espacio, Boecio no dio la demostración. Transmitió así el desafío de la cuadratura del círculo junto con fragmentos de geometría aparentemente útiles para realizarlo. Los europeos se mantuvieron en la desventurada tarea hasta la Ilustración. Finalmente, en 1775, la Academia de Ciencias de París, harta de la tarea de detectar las falacias en las muchas soluciones que se le presentaron, se negó a tener nada más que ver con los cuadrados del círculo.