Respuesta inelástica
El modo anterior de expresar [σ] en términos de [S] también es válido para los sólidos que muestran respuesta viscoelástica o plástica, excepto que [S] debe considerarse no solo como una función del presente [E M] y θ pero también como dependiente de la historia previa de ambos. Suponiendo que dichos materiales muestran una respuesta elástica a los cambios de tensión repentinos o a una pequeña descarga desde un estado de deformación plástica, [S] aún puede expresarse como una derivada de f, como se indicó anteriormente, pero se entiende que la derivada se toma con respecto a un elástico variación de deformación y se debe tomar a θ fijo y con deformación inelástica previa e historial de temperatura fijos. Tal dependencia de la historia a veces se representa como una dependencia de f en variables de estado interno cuyas leyes de evolución son parte de la descripción constitutiva inelástica. También hay modelos más simples de respuesta inelástica, y las formas más comúnmente empleadas para la plasticidad y la fluencia en sólidos isotrópicos se presentan a continuación.
Para una buena aproximación, la deformación plástica de los sólidos cristalinos no causa cambios en el volumen; y los cambios hidrostáticos en la tensión, que equivalen a un cambio igual de todas las tensiones normales, no tienen efecto en el flujo de plástico, al menos para los cambios que son del mismo orden o magnitud que la resistencia del sólido en el corte. Por lo tanto, la respuesta plástica generalmente se formula en términos de esfuerzo desviador, que se define por τ ij = σ ij - δ ij (σ 11 + σ 22 + σ 33) / 3. Siguiendo a Richard von Mises, en un procedimiento que se encuentra moderadamente de acuerdo con el experimento, la relación de flujo plástico se formula en términos de la segunda invariante del estrés desviador, comúnmente reescrita como
y llamó el esfuerzo de tensión equivalente. La definición se realiza de modo que, para un estado de tensión uniaxial, σ sea igual al esfuerzo de tracción, y la relación de esfuerzo-deformación para los estados de esfuerzo general se formula en términos de datos de la prueba de tracción. En particular, una deformación plástica ε p en una prueba de tensión uniaxial se define a partir de ε p = ε - σ / E, donde ε se interpreta como la deformación en la prueba de tracción de acuerdo con la definición logarítmica ε = lnλ, el módulo elástico E es se supone que permanece sin cambios con la deformación, y σ / E << 1.
Por lo tanto, en la versión de la teoría de la plasticidad independiente de la velocidad, se supone que los datos de tracción (o compresión, con reversiones de signo apropiadas) de una prueba de carga monotónica definen una función ε p (σ). En las versiones de la teoría de la deformación viscoplástica o de alta temperatura, los datos de tracción se interpretan para definir dε P / dt como una función de σ en el caso más simple, que representa, por ejemplo, la deformación secundaria, y como una función de σ y ε p en las teorías destinado a representar efectos de fluencia transitorios o respuesta sensible a la velocidad a temperaturas más bajas. Considere primero el modelo de material plástico rígido en el que se ignora por completo la deformabilidad elástica, ya que a veces es apropiado para problemas de flujo de plástico grande, como la formación de metal o la deformación a largo plazo en el manto de la Tierra o para el análisis de cargas de colapso plástico en estructuras. La tasa de tensor de deformación D ij está definida por 2D ij = ∂v i / ∂x j + ∂v j / ∂x i, y en el caso de plástico rígido [D] puede equipararse a lo que puede considerarse su parte plástica [D p], dado como D p / ij = 3 (dε p / dt) τ ij / 2σ. Los factores numéricos aseguran la concordancia entre D p / 11 y dε p / dt para la tensión uniaxial en la dirección 1. Además, la ecuación implica que
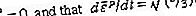
que debe integrarse sobre el historial anterior para obtener ε p como se requiere para los modelos viscoplásticos en los que dε p / dt es una función de σ y ε p. En la versión independiente de la velocidad, [D p] se define como cero siempre que σ sea menor que el valor más alto alcanzado en el historial anterior o cuando el valor actual de σ sea el valor más alto pero dσ / dt <0. (En el contexto plástico elástico, esto significa que la "descarga" implica solo una respuesta elástica.) Para el sólido idealmente plástico, que está idealizado para poder fluir sin aumentar el esfuerzo cuando σ es igual al límite elástico, dε p / dt es considerado como un parámetro indeterminado pero necesariamente no negativo, que puede determinarse (a veces no de manera exclusiva) solo a través de la solución completa de un problema de valor límite de mecánica sólida.
El modelo de material plástico elástico se formula escribiendo D ij = D e / ij + D p / ij, donde D p / ij se da en términos de tensión y posiblemente tasa de tensión como anteriormente y donde las tasas de deformación elástica [D e] están relacionadas con las tensiones por la expresión elástica lineal habitual D e / ij = (1 + ν) σ ij * / E - νδ ij (σ 11 * + σ 22 * + σ 33 *) / E. Aquí las tasas de estrés se expresan como las tasas de co-rotación de Jaumann

es una derivada que sigue el movimiento de un punto material y donde el giro Ω ij está definido por 2Ω ij = ∂v i / ∂x j - ∂v j / ∂x i. Las tasas de tensión de co-rotación son las calculadas por un observador que gira con la velocidad angular promedio de un elemento material. La parte elástica de la relación tensión-deformación debe ser consistente con la existencia de una energía libre f, como se discutió anteriormente. Esto no se cumple estrictamente con la forma que se acaba de dar, pero las diferencias entre ella y la que es consistente de esa manera implica términos adicionales que están en el orden de σ / E 2 veces el σ kl * y son insignificantes en casos típicos en los que se utiliza la teoría, ya que σ / E suele ser una fracción extremadamente pequeña de la unidad, por ejemplo, 10 −4 a 10 −2. Una versión de la teoría de pequeña tensión es de uso común para fines de análisis de tensiones de plástico elástico. En estos casos, [D] se reemplaza con ∂ [ε (X, t)] / ∂t, donde [ε] es el tensor de tensión pequeña, ∂ / ∂x con ∂ / ∂X en todas las ecuaciones, y [σ *] con ∂ [σ (X, t)] / ∂t. Los dos últimos pasos no siempre pueden justificarse, incluso en casos de tensión muy pequeña cuando, por ejemplo, en un material independiente de la velocidad, dσ / dε p no es grande en comparación con σ o cuando las velocidades de rotación de las fibras del material pueden ser mucho mayores. que las tasas de estiramiento, lo cual es una preocupación para los problemas de pandeo incluso en sólidos puramente elásticos.