Análisis tensorial, rama de las matemáticas relacionada con las relaciones o leyes que siguen siendo válidas independientemente del sistema de coordenadas utilizado para especificar las cantidades. Tales relaciones se llaman covariantes. Los tensores se inventaron como una extensión de vectores para formalizar la manipulación de entidades geométricas que surgen en el estudio de las variedades matemáticas.
Un vector es una entidad que tiene magnitud y dirección; Es representable por un dibujo de una flecha, y se combina con entidades similares de acuerdo con la ley de paralelogramo. Debido a esa ley, un vector tiene componentes, un conjunto diferente para cada sistema de coordenadas. Cuando se cambia el sistema de coordenadas, los componentes del vector cambian de acuerdo con una ley matemática de transformación deducible de la ley de paralelogramo. Esta ley de transformación de los componentes tiene dos propiedades importantes. Primero, después de una secuencia de cambios que terminan en el sistema de coordenadas original, los componentes del vector serán los mismos que al principio. En segundo lugar, las relaciones entre los vectores, por ejemplo, tres vectores U, V, W, de modo que 2U + 5V = 4W, estarán presentes en los componentes independientemente del sistema de coordenadas.
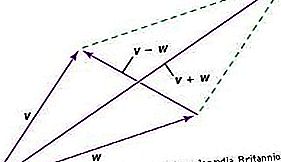
Por lo tanto, un vector puede considerarse como una entidad que, en el espacio n-dimensional, tiene n componentes que se transforman de acuerdo con una ley específica de transformación que tiene las propiedades anteriores. El vector en sí es una entidad objetiva independiente de las coordenadas, pero se trata en términos de componentes con todos los sistemas de coordenadas en pie de igualdad.
Sin insistir en una imagen pictórica, un tensor se define como una entidad objetiva que tiene componentes que cambian de acuerdo con una ley de transformación que es una generalización de la ley de transformación vectorial pero que retiene las dos propiedades clave de esa ley. Por conveniencia, las coordenadas generalmente están numeradas del 1 al n, y cada componente de un tensor se denota con una letra que tiene superíndices y subíndices, cada uno de los cuales toma independientemente los valores 1 a n. Por lo tanto, un tensor representado por los componentes T ab c tendría n 3 componentes como los valores de a, byc van de 1 a n. Los escalares y los vectores constituyen casos especiales de tensores, el primero posee solo un componente por sistema de coordenadas y el segundo posee n. Cualquier relación lineal entre componentes tensoriales, como 7R a bcd + 2S a bcd - 3T a bcd = 0, si es válida en un sistema de coordenadas, es válida en todos y, por lo tanto, representa una relación objetiva e independiente de los sistemas de coordenadas a pesar de falta de una representación pictórica
Dos tensores, llamados tensor métrico y tensor de curvatura, son de particular interés. El tensor métrico se usa, por ejemplo, para convertir componentes de vectores en magnitudes de vectores. Para simplificar, considere el caso bidimensional con coordenadas perpendiculares simples. Deje que el vector V tenga los componentes V 1, V 2. Luego, mediante el teorema de Pitágoras aplicado al triángulo rectángulo OAP, el cuadrado de la magnitud de V viene dado por OP 2 = (V 1) 2 + (V 2) 2.

Oculto en esta ecuación está el tensor métrico. Está oculto porque aquí consta de 0 y 1 que no están escritos. Si la ecuación se reescribe en la forma OP 2 = 1 (V 1) 2 + 0V 1 V 2 + 0V 2 V 1 + 1 (V 2) 2, el conjunto completo de componentes (1, 0, 0, 1) del tensor métrico es aparente. Si se utilizan coordenadas oblicuas, la fórmula para OP 2 toma la forma más general OP 2 = g 11 (V 1) 2 + g 12 V 1 V 2 + g 21 V 2 V 1 + g 22 (V 2) 2, las cantidades g 11, g 12, g 21, g 22 son los nuevos componentes del tensor métrico.
Fuera del tensor métrico es posible construir un tensor complicado, llamado tensor de curvatura, que representa los diversos aspectos de la curvatura intrínseca del espacio n-dimensional al que pertenece.
Los tensores tienen muchas aplicaciones en geometría y física. Al crear su teoría general de la relatividad, Albert Einstein argumentó que las leyes de la física deben ser las mismas sin importar qué sistema de coordenadas se use. Esto lo llevó a expresar esas leyes en términos de ecuaciones tensoras. Ya se sabía por su teoría especial de la relatividad que el tiempo y el espacio están tan estrechamente relacionados que constituyen un espacio-tiempo de cuatro dimensiones indivisible. Einstein postuló que la gravitación debería representarse únicamente en términos del tensor métrico del espacio-tiempo tetradimensional. Para expresar la ley relativista de la gravitación, tenía como componentes básicos el tensor métrico y el tensor de curvatura formado a partir de él. Una vez que decidió limitarse a estos bloques de construcción, su escasez lo condujo a una ecuación tensora esencialmente única para la ley de la gravitación, en la que la gravitación surgió no como una fuerza sino como una manifestación de la curvatura del espacio-tiempo.
Si bien los tensores se habían estudiado anteriormente, fue el éxito de la teoría general de la relatividad de Einstein lo que generó el actual interés generalizado de matemáticos y físicos en los tensores y sus aplicaciones.